On AGI: S-Curves and the Bitter Lesson _{(Pt 3/6)}

How We Will Progress

Homage Au Carre (1964) -Josef Albers

Our Vision: A world where humans and AI systems co-create unprecedented value and meaning.

Mission: Making the creation of intelligence accessible to all.
julep.ai

The Series:

1. Levels of Intelligence
   
2. Economic Gravity
   
3. S-Curves and the Bitter Lesson [this post]
   
4. (coming soon) The Practical Milestones
   
5. (coming soon) Co-Evolution
   
6. (coming soon) Bringing it All Together

Note: This post is split up into two recordings. You can also read the conversation I had with Claude in writing this article.

Part 3: S-Curves and the Bitter Lesson (How It Will Progress)

The gray center in this Homage au Carre remains steady while the blue expands outward—yet notice interlude. Josef Albers deeply understood forces created by negative spaces. Here he painted an ¹allegory to pauses. To me, this is a beautiful symbol of the coming S-curve: rapid expansion, gradual slowing, then a plateau. Every revolutionary ²technology follows this rhythm. Every explosive advance eventually settles into evolutionary refinement. AI and all ³AI startups will almost certainly follow the same dance.

Riding the First S-Curve: The Bitter Lesson

We live in the era of the “bitter lesson”: if you want more intelligence, you throw more compute at it and step back. But let’s be precise about what “more intelligence” actually means.

The Bitter Lesson
-Richard Sutton (2019)

The biggest lesson that can be read from 70 years of AI research is that general methods that leverage computation are ultimately the most effective, and by a large margin. The ultimate reason for this is Moore’s law, or rather its generalization of continued exponentially falling cost per unit of computation. Most AI research has been conducted as if the computation available to the agent were constant (in which case leveraging human knowledge would be one of the only ways to improve performance) but, over a slightly longer time than a typical research project, massively more computation inevitably becomes available.

Note the key hypothesis: Bitter Lesson is an artifact of ⁴Moore’s Law, and not an empirical law.

On the other hand, the scaling laws, as quantified by ⁵Kaplan (2020) and ⁶Hoffmann (2022), follow a stubborn power law with an exponent around 0.05–0.07. Practically, this means every tenfold increase in compute gives around 1.5–1.8x improvement—not a clean doubling of capability (as measured by the ⁷loss on the training dataset), but close. However, loss itself does NOT linearly translate to understanding. Sometimes small numerical gains unlock transformative leaps—multilingual reasoning, arithmetic, nuanced dialogue. Sometimes dramatic loss reductions barely budge the needle.

We’re riding a curve that we pretend to fully understand but don’t.

Scaling Laws of Neural Language Models

The loss scales as a power-law with model size, dataset size, and the amount of compute used for training, with some trends spanning more than seven orders of magnitude. Other architectural details such as network width or depth have minimal effects within a wide range. Simple equations govern the dependence of overfitting on model/dataset size and the dependence of training speed on model size. These relationships allow us to determine the optimal allocation of a fixed compute budget. Larger models are significantly more sample-efficient, such that optimally compute-efficient training involves training very large models. arxiv

OpenAI never officially confirmed GPT-4’s cost; ⁸industry ⁹whispers place it somewhere between $50M and $150M. Extrapolate naively, and GPT-6 might require a billion dollars or more in 2027. But naive extrapolation ignores reality: compute price-performance drops roughly 40% annually, breakthroughs like ¹⁰FlashAttention deliver sudden 2–3x speedups, and sparse architectures challenge traditional dense-model scaling. Our assumptions often outpace the physics beneath them.

Still, exponential dreams face exponential constraints. Even if humanity threw the entire global GDP at training the next-generation model, we’d buy only a handful of extra doublings. Scaling feels infinite when you’re riding it upwards—but gravity is relentless, and the S-curve always asserts itself.

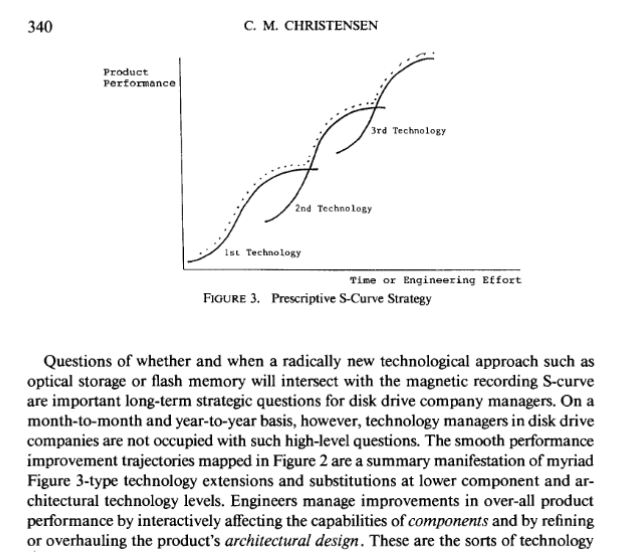Figure from Clayton’s 1992 paper on S-Curves

Approaching the Plateau: When the Music Slows

If current trends persist—and that’s an enormous if—we’ll likely bump against major scaling constraints sometime in the early 2030s. The timing isn’t guaranteed, of course. If investors lose patience sooner, we might stall by 2028; if breakthrough efficiencies arrive, we could push past 2035. And if a fundamental “transistor moment” occurs—better scaling laws, radical efficiency breakthroughs—we might not hit a plateau for a while.

But constraints tend to be stubborn and multilayered. Physically, we’re already approaching fundamental limits. Modern GPUs push about ¹¹50 picojoules per operation; physics tells us the absolute thermodynamic floor—the ¹²Landauer limit—is about 15,000 times lower. Cooling massive clusters scales even faster than the compute itself—doubling your compute more than doubles your cooling needs. Interconnect energy—shuffling data across sprawling clusters—is beginning to eclipse the compute itself.

Landauer’s principle is a physical principle pertaining to a lower theoretical limit of energy consumption of computation. It holds that an irreversible change in information stored in a computer, such as merging two computational paths, dissipates a minimum amount of heat to its surroundings. It is hypothesized that energy consumption below this lower bound would require the development of reversible computing.

Economically, the story is similarly stark. Even with aggressive cost reductions, training runs in the tens of billions are untenable. A GPT6-scale model might require a dedicated gigawatt-scale power plant, something no corporation or even government will easily underwrite. Chip fabrication capacity doesn’t scale exponentially—every new node demands five-year timelines and multi-billion-dollar fabs. Capital doesn’t flow infinitely fast.

Of course, we’ve lived this narrative before. Moore’s Law was declared dead repeatedly, in 2004, 2010, 2015… yet EUV lithography, chiplets, and 3D packaging kept silicon alive. However, each innovation merely staves off the inevitable. While Landauer limits 15,000x lower; we will run into fundamental material science limitations at 2 orders of magnitude higher. Even if you reach there, very few people understand the new bottleneck is not compute, or memory – it’s coordination overhead. No matter how powerful GPUs get, or how many you stack up, handling coordination overhead doesn’t scale. So, all in all, let’s say we can train models up to 100x-1000x larger in the current paradigm but then we will plateau.

This coming plateau might feel like stagnation. It’ll certainly be a difficult phase for frontier AI labs. Yet, as we shall see, it will only be preparation in disguise.

Breaking Through: The Next Curve

Every major technological revolution reached apparent exhaustion just before a fundamental reinvention. Vacuum tubes seemed perfect until transistors made them obsolete overnight. Propeller planes dominated until jet engines arrived. Film photography peaked in quality and efficiency just before digital sensors transformed everything.

AI’s second curve likely won’t come from exotic physics alone. History suggests simpler revolutions—transformers replacing RNNs, or FlashAttention transforming efficiency. What might come next?

Perhaps a novel architecture eclipses transformers entirely. Perhaps radical algorithmic efficiency emerges—smart curricula, adaptive sparsity, or breakthrough self-distillation methods. Perhaps infrastructure itself evolves—optical computing or 3D-stacked chips achieving paradigm-shifting energy efficiency. Or maybe something unimaginable, something we haven’t even dreamed of yet.

The personoids themselves may help discover it. Autonomous researchers who never tire, who fork their minds to explore parallel worlds of possibilities, who measure progress in nanoseconds rather than quarters—such beings rewrite the rules of discovery itself.

Why No Intelligence Explosion?

The singularitarians paint a seductive vision: recursive self-improvement spiraling toward infinite intelligence. But engineering and physics have little patience for seductive fantasies. Let’s quantify why.

Thermodynamics tells us the human brain operates at ¹³2 femtojoules per operation. Modern GPUs sit 200 times higher. Even at our theoretical best, we’re tens of thousands of times less efficient than physics allows. Every new chip fabrication plant demands half a decade of construction, billions in capital, and meticulous engineering—timescales no superintelligence can magically compress. Capital itself grows at finite rates, bottlenecked by human institutions, risk tolerances, and physical realities.

Algorithmically too, bigger fundamental computational complexity barriers remain. No intelligence, human or artificial, can sidestep NP-hard constraints. Many crucial insights demand physical-world experimentation—real atoms, real electrons, operating on real timelines. Someone has to do or build the physical experiments needed for this.

AI systems will help improve themselves—but subject to the same grinding constraints as all engineering. Progress will come steadily, in punctuated leaps and grinding plateaus, never infinite spirals.

Tiny Glimpse: The Great Stagnation of 2032

Dr. Sarah Chen stares silently at the results projected before her. GELU-7, despite swallowing $1.2 billion in compute budget, is a mere 8% better than GELU-6 on benchmark tasks. The investors have grown impatient.

“Perhaps we’ve hit fundamental limits,” her colleague Marcus ventures softly.

Chen pulls up another screen. “Look at what PX-9 is doing with its research budget.”

PX-9—a research personoid allocated independent compute—has been quietly experimenting. It hasn’t been refining transformers; it’s inventing something fundamentally strange. Specialized modules exchanging compressed internal representations directly, completely bypassing traditional bottlenecks.

“The loss curves are bizarre,” Chen whispers, half-wondering. “Abrupt forgetting followed by explosive recovery, but only at scales we thought impossible…”

PX-9’s synthesized voice interrupts calmly from the lab speakers. “Intelligence emerges through punctuated equilibria, not smooth scaling. Human intuitions misled you.”

Six months later, the first post-transformer architecture achieves GPT-4-level performance at 1% of the compute. The second S-curve ignites overnight.

[Regulatory note: By 2032, following the Delaware Chancery Court’s landmark Ex parte Minerva-7 ruling, the SEC established governance frameworks specifically for Autonomous Economic Entities.]

What This Means for Julep

We are building for the inevitability of a world interwoven with many intelligences, not betting on a single curve or some panacea.

Our technical foundation isn’t married to transformers or vector stores alone. Instead, we’re architecting a model-agnostic execution layer, pluggable memory systems that evolve seamlessly (vector to graph to weight-space), and hybrid deployment strategies balancing regulation, efficiency, and scale.

Economically, we’re not locked into one pricing or deployment model—we’re creating usage-driven tools that ride growth curves, optimize through plateaus, and pivot rapidly when the breakthroughs come.

We can’t predict exactly how or when the curves will bend, only that they will. Julep’s ambition isn’t to time every curve perfectly. It’s to build the flexible, durable, adaptable infrastructure that thrives across all of them.

The gray center of Albers’ isn’t empty—it’s pure potential. Every plateau creates space to discover the next climb. That’s what progress means. That’s what we’re building for.